Anand Model: Theoretical Forumation and Application to Solder Joints
Michael Raba, MSc Candidate at University of Kentucky
Created: 2025-04-26 Sat 15:03
Source Paper

These are speaker notes visible only in presenter mode.
Introduction to Anand’s Unified Viscoplasticity Model (1985)
- Many metals at high temperatures experience creep and plasticity simultaneously.
- Traditional plasticity models use yield surfaces and separation rules.
- Anand proposes a unified framework to capture both phenomena without a yield condition.
- Introduces a smooth viscoplastic flow model with a single scalar resistance variable \( s \).
- Fully derived from thermodynamic principles (dissipation inequality).
- Applicable to hot working, solder behavior, and finite deformation problems.
Mapping Anand’s Section 3 to Wang’s Model
| Anand (1985) | Role | Wang (2001) | Comment |
|---|---|---|---|
| (77) \( \dot{T} = \mathbb{L} [D - D^p] - \eta \mathbb{I} \) | Elastic stress–strain–temperature relation | Not included explicitly | Elasticity assumed handled separately in FEM. |
| (78)-(80) \( D^p = \dot{\gamma}^p \frac{T'}{2\tau} \) | Plastic flow rule based on deviatoric stress | \( \dot{\varepsilon}^p = A \exp\left( -\frac{Q}{RT} \right) \left[ \sinh\left( \frac{j\sigma}{s} \right) \right]^{1/m} \) | Flow scalarized: stress–strain relation based on effective stress \( \sigma \). |
| (81)-(86) \( \dot{s} = h(\sigma, s, \theta) \dot{\varepsilon}^p - r(s, \theta) \) | Evolution of deformation resistance \( s \) | \( \dot{s} = h_0 \left( 1 - \frac{s}{s^*} \right)^a \dot{\varepsilon}^p \) | Hardening toward \( s^* \); no explicit static recovery \( r \) included. |
Main Equations of Wang’s Anand-Type Viscoplastic Model
- \[ \dot{\varepsilon}^p = A \exp\left( -\frac{Q}{RT} \right) \left[ \sinh\left( \frac{j \sigma}{s} \right) \right]^{1/m} \]
- Plastic strain rate increases with stress and temperature.
- No explicit yield surface; flow occurs at all nonzero stresses.
- \[ s^* = \hat{s} \left( \frac{\dot{\varepsilon}^p}{A} \exp\left( \frac{Q}{RT} \right) \right)^n \]
- Defines the steady-state value that \( s \) evolves toward.
- Depends on strain rate and temperature.
- \[ \dot{s} = h_0 \left| 1 - \frac{s}{s^*} \right|^a \, \text{sign}\left(1 - \frac{s}{s^*}\right) \dot{\varepsilon}^p \]
- Describes dynamic hardening and softening of the material.
- \( s \) evolves depending on proximity to \( s^* \) and flow activity.
Parameter m for Sixty tin forty lead solder
- As \( m \to 0 \), the material behaves almost like rate-independent plasticity: very sharp yielding.
- As \( m \to 1 \), the material flows smoothly with almost no sharp yield point (strong rate sensitivity).
Understanding When \( s^* \) is Fixed in Anand’s Model
- Constant \( \dot{\varepsilon}^p \) and \( T \):
- \( s^* \) can be treated as approximately fixed
- Varying \( \dot{\varepsilon}^p \) or \( T \):
- \( s^* \) evolves and must be updated dynamically
In Wang's paper and Anand's original model, \( s^* \) is given by:
\[ s^* = \hat{s} \left( \frac{\dot{\varepsilon}^p}{A} e^{Q/RT} \right)^n \]
\( s^* \) explicitly depends on strain rate ( \( \dot{\varepsilon}^p \) ) and temperature ( \( T \) ).
Anand Viscoplasticity Constants for 60Sn40Pb
Values are from correspond to 60Sn40Pb solder parameters used in Anand's model:
- \( S_0 \): Initial deformation resistance
- \( Q/R \): Activation energy over gas constant
- \( A \): Pre-exponential factor for flow rate
- \( \xi \): Multiplier of stress inside sinh
- \( m \): Strain rate sensitivity of stress
- \( h_0 \): Hardening/softening constant
- \( \hat{s} \): Coefficient for saturation stress
- \( n \): Strain rate sensitivity of saturation
- \( a \): Strain rate sensitivity of hardening or softening
- \( S_0 = 5.633 \times 10^7 \) Pa
- \( Q/R = 10830 \) K
- \( A = 1.49 \times 10^7 \) s\(^{-1}\)
- \( \xi = 11 \)
- \( m = 0.303 \)
- \( h_0 = 2.6408 \times 10^9 \) Pa
- \( \hat{s} = 8.042 \times 10^7 \) Pa
- \( n = 0.0231 \)
- \( a = 1.34 \)
These constants match Wang's paper for modeling 60Sn40Pb viscoplasticity.
Internal Variable \( s \) in Anand and Wang Models
- Internal variable \( s \) evolves dynamically:
- \( \dot{s} = h(\sigma, s, T) \dot{\varepsilon}^p - \phi(s, T) \)
- Describes both hardening and recovery processes.
- No fixed saturation \( s^* \) assumed.
- Defines a practical saturation stress \( s^* \):
- \( s^* = \hat{s} \left( \frac{\dot{\varepsilon}^p}{A} e^{Q/RT} \right)^n \)
- Relates \( s^* \) to strain rate and temperature.
- Simplifies parameter extraction for finite element simulations.
- At steady-state plastic flow, Wang assumes:
- \( s \approx \frac{\sigma}{\xi} \)
- \( \xi \) is the stress multiplier in the sinh function (called \( j \)).
- Provides a direct link between observed stress and internal variable \( s \).
Case Study: Wang (2001)

DOI: 10.1115/1.1371781
- Applies Anand’s unified viscoplastic framework to model solder behavior.
- Focuses on thermal cycling fatigue and rate-dependent deformation.
- Demonstrates how Anand's model can be reduced and fitted from experiments.
- Helps transition the theory into engineering-scale implementation.
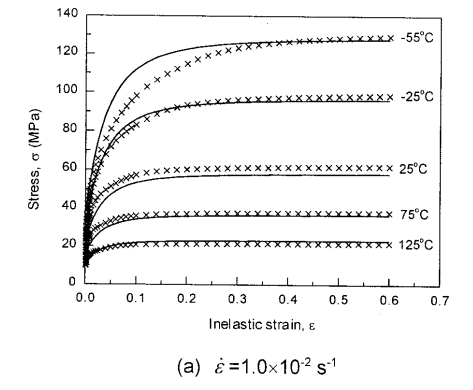
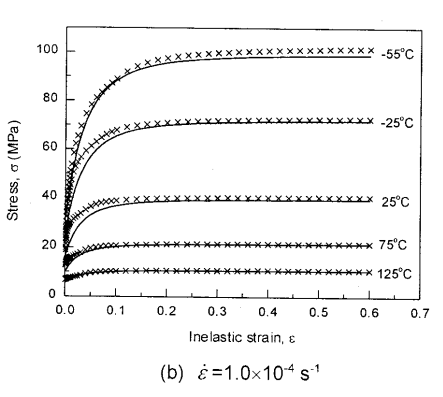
Comparing Anand Model Predictions at Two Strain Rates
- Top Graph (a): \( \dot{\varepsilon} = 10^{-2} \, \text{s}^{-1} \)
- High strain rate → higher stress
- Recovery negligible → pronounced hardening
- Bottom Graph (b): \( \dot{\varepsilon} = 10^{-4} \, \text{s}^{-1} \)
- Lower strain rate → lower stress at same strain
- Recovery and creep effects more significant
Model Accuracy: Lines = model prediction, X = experimental data
- “At lower strain rates, recovery dominates… the stress levels off early.”
- “At high strain rates, hardening dominates, and the stress grows continuously.”
Anand’s model smoothly captures strain-rate and temperature dependence of solder materials.
Anand Approximation
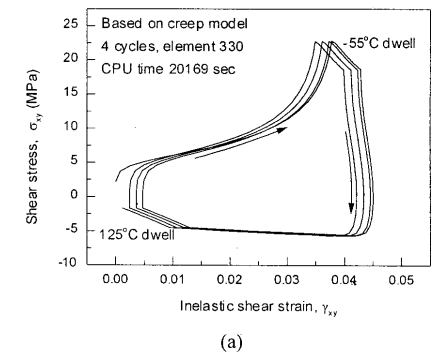
- FEA Ready: Smooth equations, Jaumann derivatives, and rate-dependence make it suitable for cyclic thermal loads.
- Path Dependence & Hysteresis: Anand’s model shows how evolving internal variables (like \( s \), \( \bar{\mathbf{B}} \)) naturally reproduce load history and hysteresis effects — a cornerstone of modern inelasticity.
- Path Dependence: Internal variables like \( s \), \( \bar{\mathbf{B}} \) evolve, showing hysteresis and memory effects — core ideas in inelasticity.
- Rate Sensitivity: The Anand model embodies a regularized flow rule, helping avoid ill-posedness
- Thermomechanical Coupling: Graduate models often simplify heat effects; Anand incorporates temperature-dependent recovery and strain rates realistically.
What If the Material Were Not Viscoplastic?
- No strain rate sensitivity: All curves would collapse onto a single stress–strain curve, regardless of temperature.
- Sharp yield point: Stress would remain low until a threshold is reached, then suddenly rise — no smooth buildup.
- Post-yield response: Would likely show perfectly plastic or linear hardening behavior, independent of rate.
- This behavior mirrors rate-independent J2 plasticity with isotropic hardening.
- In graduate courses, it corresponds to models with yield surfaces and flow rules only activated above yield stress.
- Contrasts Anand’s approach, where flow begins smoothly at any stress, blending creep and plasticity into one.
How Wang Simplifies Anand’s Thermodynamic Model
- Defines a free energy \( \psi \) based on elastic strain and internal variables.
- Tracks entropy production \( \mathcal{D} \) to guarantee positive dissipation.
- Uses dissipation potential to derive flow rule and internal variable evolution.
- Explicit hardening and softening terms driven by thermodynamic forces.
- Introduces a saturation stress \( s^* \) that depends on \( \dot{\varepsilon}^p \) and \( T \).
- Directly evolves \( s \to s^* \) without explicitly tracking entropy or free energy.
- Positive dissipation guaranteed by construction (no free energy increase).
- Simplifies parameter extraction and implementation for FEA models.
- Anand: Thermodynamic forces drive \( \dot{s} \); complex but fundamental.
- Wang: \( s \) moves toward \( s^* \) with flow rate; simpler, but still thermodynamically consistent.
- Result: Wang’s model is easier to code and fit to data without losing physical realism.
Breakthrough Features of Anand’s Viscoplastic Model
- Plastic flow occurs at any stress level.
- No von Mises yield or loading/unloading logic.
- Enables unified creep–plasticity modeling.
- Represents resistance to inelastic flow.
- Captures hardening, softening, and recovery.
- Governs evolution in Eq. (86).
- Grounded in reduced dissipation inequality (Eq. 28).
- Ensures entropy production and realism.
- Built from stress–strain conjugacy, energy balance.
- Uses Jaumann derivatives for stress and backstress.
- Maintains frame invariance (Eqs. 63, 65–66).
- Essential for rotating frames in FEA.
- 1D model extractable from uniaxial data.
- Wang (2001) shows direct parameter fitting.
- Equations (77–86) ready for FE implementation.
Anand's model unifies physical laws, experiment, and computation in one robust viscoplastic framework.
Formulation pipeline for Anand’s viscoplastic model
This flow ensures Anand’s model is thermodynamically consistent and computationally implementable.
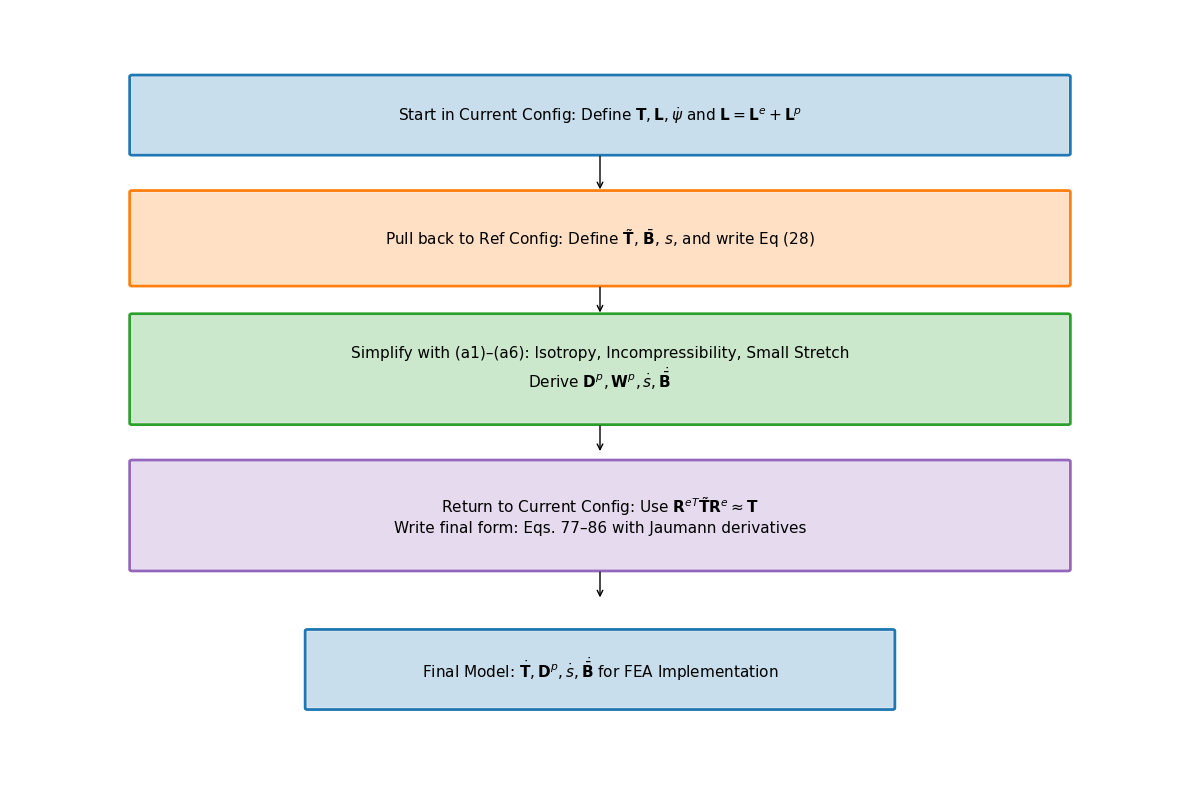
Broad Strokes of Anand’s Unified Viscoplastic Model (1985)
1. Modeling Goal
- Unify inelastic deformation: creep + plasticity
- Avoid yield surfaces and loading/unloading rules
- Support large deformation and high temperatures
2. State Variables
\[ \{ \mathbf{T}, \theta, \mathbf{g}, \bar{\mathbf{B}}, s \} \]- Stress, temperature, and temperature gradient
- Backstress-like tensor \( \bar{\mathbf{B}} \)
- Scalar internal resistance \( s \)
3. Reference Configuration Formulation
- Switch to relaxed frame (material configuration)
- Formulate stress power and entropy production
- Arrive at dissipation inequality (Eq. 28)
️ 4. Thermodynamic Constraints
- Apply (i)-(iv): entropy, energy, heat flow laws
- Use assumptions (a1)–(a5): small elastic stretch, isotropy, incompressibility
- Restrict response functions \( \bar{\mathbf{B}}, s, \dot{s} \)
5. Simplified Constitutive Equations
- Polynomial-based evolution for \( \bar{\mathbf{B}} \) and \( s \)
- Simplified plastic flow and hardening response
6. Back to Current Configuration
- Use small elastic stretch:
- Reformulate in spatial frame for FEA compatibility
7. Final Model (Eqs. 77–86)
- Includes stress rate, flow rule, and hardening law
- Unified viscoplastic response — smooth & thermally sensitive
- Ready for implementation in FEA solvers
Thermodynamic Foundations of Anand’s Model
- \(\dot{\psi} = \frac{\partial \psi}{\partial \mathbf{E}^e} : \dot{\mathbf{E}}^e + \frac{\partial \psi}{\partial s} \dot{s}\)
- \(\eta_r = -\frac{\partial \psi}{\partial \theta}\)
- \(\Rightarrow \dot{\psi} - \mathbf{T}:\dot{\mathbf{E}}^e - \eta_r\dot{\theta} \leq 0\)
- Result: All response functions must respect the second law of thermodynamics.
- (a1) Objective stress measures (e.g., Jaumann rate)
- (a2) Isotropy in material response
- (a3) Incompressibility of plastic flow
- (a4) Free energy function is additively decomposed
- (a5) Temperature dependence enters through specific variables
- (a6) Separation of mechanical and thermal effects is approximated
- \( A \) – Pre-exponential factor for flow rate.
- \( Q \) – Activation energy (units of energy/mol).
- \( \xi \) – Stress multiplier inside the sinh() law.
- \( m \) – Strain rate sensitivity exponent.
- \( \dot{\varepsilon}^p \) – Effective plastic strain rate.
- \( \bar{\sigma} \) – Effective (von Mises) stress.
- \( \mathbb{L} \) – Elastic stiffness tensor.
- \( \Pi \) – Stress-temperature coupling tensor.
- \( \bar{\mathbf{T}} \) – Kirchhoff stress (reference frame).
- \( \mathbf{D}, \mathbf{D}^p \) – Total and plastic strain rate tensors.
- \( s \) – Isotropic strength (scalar resistance variable).
- \( \hat{s} \) – Saturation value for \( s \).
- \( n \) – Sensitivity of \( \hat{s} \) to strain rate.
- \( h_0 \) – Hardening modulus coefficient.
- \( a \) – Exponent controlling recovery rate of \( s \).
- \( \xi_1, \xi_2 \) – Coefficients for driving terms in \( \dot{\bar{\mathbf{B}}} \).
- \( \mathbf{W}^p \) – Plastic spin tensor.
- \( b(\bar{\tau}_b) \) – Oscillation control function (for shear stability).
How Anand’s Model Unifies Creep and Plasticity
Creep-Driven Terms
Eq. (84):
\[
\dot{\bar{\varepsilon}}^p = g(\bar{\sigma}, s, \theta)
\]
Steady-state creep rate governed by stress and temperature.
Eq. (86):
\[
\dot{s} = h(\bar{\sigma}, s, \theta)\dot{\bar{\varepsilon}}^p - r(s, \theta)
\]
Captures transient creep via thermal recovery.
Hyperbolic Sine Flow Law:
\[
\dot{\bar{\varepsilon}}^p \propto \sinh\left(\frac{\xi \sigma}{s}\right)^{1/m}
\]
Models thermally activated dislocation motion.
Smooth rate-dependence:
Enables creep-like flow even at low stress without a sharp yield point.
Plasticity-Driven Terms
Internal variable \( s \):
Represents isotropic resistance; evolves with plastic strain.
Eq. (83):
\[
\mathbf{D}^p = \dot{\bar{\varepsilon}}^p \left\{ \bar{\sigma}^{-1} \mathbf{T}^r \right\}
\]
Plastic flow direction set by stress deviator.
Eq. (85):
\[
\dot{s} = \tilde{g}(\bar{\sigma}, s, \theta)
\]
Tracks hardening-like resistance from internal variable.
No explicit yield surface:
Still captures hardening and saturation as in classical models.
Interpretation of Intermediate Terms (S3 & S4)
- \(\mathbf{L}^p = x_1 \tilde{\mathbf{T}}' + \eta_1(\tilde{\mathbf{T}}' \mathbf{B} - \mathbf{B} \tilde{\mathbf{T}}')\)
- Represents viscoplastic flow direction and includes kinematic backstress effect.
- \(\dot{\mathbf{B}} = \xi_1 \tilde{\mathbf{T}}' + \xi_2 \mathbf{B}\)
- Linear evolution of internal backstress — similar to Armstrong–Frederick type models.
- \(\dot{s} = h_0 \left|1 - \frac{s}{s^*} \right|^a \cdot \text{sign}\left(1 - \frac{s}{s^*} \right) \dot{\varepsilon}^p\)
- Captures isotropic hardening/softening and saturates toward \( s^* \).
- Gives physical intuition: backstress = directional memory, \(s\) = isotropic “strength”.
- Helps map terms to graduate plasticity topics (e.g., hardening laws, associative flow).
- Facilitates debugging in FEA — parameters must align with observed behavior.
- Clarifies why Anand’s model is more than just a curve-fit: it encodes mechanics.
Thermodynamic Foundations of Anand’s Model
- \(\dot{\psi} = \frac{\partial \psi}{\partial \mathbf{E}^e} : \dot{\mathbf{E}}^e + \frac{\partial \psi}{\partial s} \dot{s}\)
- \(\eta_r = -\frac{\partial \psi}{\partial \theta}\)
- \(\Rightarrow \dot{\psi} - \mathbf{T}:\dot{\mathbf{E}}^e - \eta_r\dot{\theta} \leq 0\)
- Result: All response functions must respect the second law of thermodynamics.
- (a1) Objective stress measures (e.g., Jaumann rate)
- (a2) Isotropy in material response
- (a3) Incompressibility of plastic flow
- (a4) Free energy function is additively decomposed
- (a5) Temperature dependence enters through specific variables
- (a6) Separation of mechanical and thermal effects is approximated
How Anand’s Model Unifies Creep and Plasticity
Creep-Driven Terms
Eq. (84):
\[
\dot{\bar{\varepsilon}}^p = g(\bar{\sigma}, s, \theta)
\]
Steady-state creep rate governed by stress and temperature.
Eq. (86):
\[
\dot{s} = h(\bar{\sigma}, s, \theta)\dot{\bar{\varepsilon}}^p - r(s, \theta)
\]
Captures transient creep via thermal recovery.
Hyperbolic Sine Flow Law:
\[
\dot{\bar{\varepsilon}}^p \propto \sinh\left(\frac{\xi \sigma}{s}\right)^{1/m}
\]
Models thermally activated dislocation motion.
Smooth rate-dependence:
Enables creep-like flow even at low stress without a sharp yield point.
Plasticity-Driven Terms
Internal variable \( s \):
Represents isotropic resistance; evolves with plastic strain.
Eq. (83):
\[
\mathbf{D}^p = \dot{\bar{\varepsilon}}^p \left\{ \bar{\sigma}^{-1} \mathbf{T}^r \right\}
\]
Plastic flow direction set by stress deviator.
Eq. (85):
\[
\dot{s} = \tilde{g}(\bar{\sigma}, s, \theta)
\]
Tracks hardening-like resistance from internal variable.
No explicit yield surface:
Still captures hardening and saturation as in classical models.
Summary of Anand’s Model
The model treats rate-dependent creep and rate-independent plasticity as a single, smooth phenomenon.
Avoids arbitrary separation of strain types.
Ideal for solder and hot-working cases.
Represents average isotropic resistance to plastic flow.
Evolves with stress and temperature.
Eliminates need for complex multi-surface rules.
Captures power-law breakdown and nonlinear rate sensitivity.
Handles thermal-cycling hysteresis where traditional plasticity fails.
No need to distinguish creep from plastic experimentally.
Parameters fit to total viscoplastic strain data.
Simplifies experimental workflow.
Uses stable backward Euler integration.
No strict stability limit.
Highly effective for long-term simulations in FEA.
The Anand model unifies both creep and plasticity into one smooth viscoplastic framework, enabling predictive modeling of time-dependent deformation with thermodynamic consistency and computational efficiency.